Question

Find the measures of the geometric parts listed below

Answer 1

Part a) The measure of angle BDC is
`m<BDC=48\°`

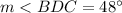
Part b) The measure of angle CPD is
`m<CPD=68\°`

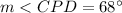
Part c) The measure of arc AD is
`arc\ AD=128\°`

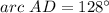
Part d) The measure of arc AB is
`arc\ AB=52\°`

Part e) The measure of arc CAD is
`arc\ CAD=276\°`

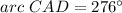
Part f) The measure of angle ABD is
`m<ABD=64\°`

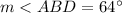
Explanation:

Part a) Find the measure of angle BDC

we know that

The inscribed angle is half that of the arc it comprises.

`m<BDC=(1)/(2)(arc\ BC)`

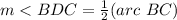
substitute the value

`m<BDC=(1)/(2)(96\°)=48\°`

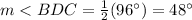
Part b) Find the measure of angle CPD

we know that

The sum of the internal angles of a triangle must be equal to 180 degrees.

so In the triangle CPD

`64\°+m<CPD+m<BDC=180\°`

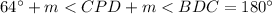
substitute the values

`64\°+m<CPD+48\°=180\°`

`m<CPD=180\°-112\°=68\°`

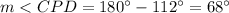
Part c) Find the measure of arc AD

we know that

The inscribed angle is half that of the arc it comprises.

`m<PCD=(1)/(2)(arc\ AD)`

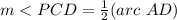
substitute the values

`64\°=(1)/(2)(arc\ AD)`

`arc\ AD=128\°`

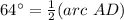
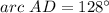
Part d) Find the measure of arc AB

Remember that BD is a diameter

so

`arc\ AB+arc\ AD=180\°` ----> the diameter divide the circle into two equal parts

`arc\ AB+128\°=180\°`

`arc\ AB=180\°-128\°=52\°`

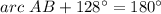
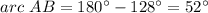
Part e) Find the measure of arc CAD

we know that

`arc\ CAD=arc\ CB+arc\ BAD`

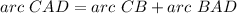
substitute the values

`arc\ CAD=96\°+180\°=276\°`

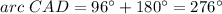
Part f) Find the measure of angle ABD

we know that

The inscribed angle is half that of the arc it comprises.

`m<ABD=(1)/(2)(arc\ AD)`

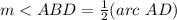
substitute the values

`m<ABD=(1)/(2)(128\°)=64\°`