Question

A 0.20-kg object attached to the end of a string swings in a vertical circle (radius = 80 cm). at the top of the circle the speed of the object is 4.5 m/s. what is the magnitude of the tension in the string at this position?

Answer 1

Tension in the string at this position: 3.1 N.

Step-by-step explanation:

Convert the radius of the circle to meters:

`r = 80\;\text{cm} = 0.80\;\text{m}`.

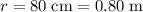What's the net force on the object?

The object is in a circular motion. As a result,

`\displaystyle \Sigma F = (m\cdot v^(2))/(r)`,

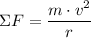where

• 
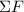  `\Sigma F` is the net force on the object,
• 
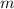  `m` is the mass of the object,
• 
  `v` is the velocity of the object, and
• 
  `r` is the radius of the circular motion.

For this object,

`\displaystyle \Sigma F = \frac{0.20* {4.5}^(2)}{0.80} = 5.0625\;\text{N}`.

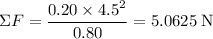The output unit of net force should be standard if the unit for mass, velocity, and radius are all standard. The net force shall always point towards the center. In this case the net force points downwards.

What are the forces on this object?

There are two forces on the object at this moment:

• Weight,
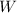  `W`, which points downwards.
  `W = m\cdot g = 0.20* 9.81 = 1.962\;\text{N}`.
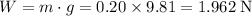• Tension,
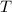  `T`, which also points downwards. The size of the tension force needs to be found.

What's the size of the tension force?

Gravity and tension points in the same direction. The size of their resultant force is the sum of the two forces. In other words,

`\Sigma F = T + W`.

`T = \Sigma F - W = 5.0625 - 1.962 = 3.1`.

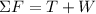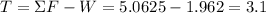All three values in this question are given with two sig. fig. Round the value of
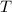`T` to the same number of significant figures.