Answer:
6.50m/s
Step-by-step explanation:
Using conservation of energy, the total energy in the system is conserved. We know that the ball has potential energy initially because it is elevated 2 meters. We also know it has kinetic energy because it is given an initial speed of 1.75 m/s. At the bottom of the ramp, it loses all potential energy and is converted directly to kinetic energy. We can model the equation as below. U is the potential energy, K is the initial kinetic energy and K' is final kinetic energy.
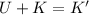
Equation for kinetic energy is
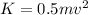
and potential energy is:
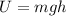
Plug these equation to the first equation and simplify (v' is final speed):
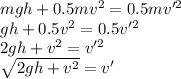
Plug in the values:

Final speed is 6.50m/s