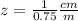Question

The diagram shows a scale drawing of a playground. In the scale drawing the playground has a length of 16 cm and a width of 8 cm. The area of the actual playground is 72 square meters what is the scale of the drawing?

Answer 1

The scale of the drawing is

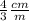`(4)/(3)(cm)/(m)` or
`(1)/(0.75)(cm)/(m)`

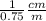
Explanation:

we know that

If two figures are similar, then the ratio of its areas is equal to the scale factor squared

Let

z-----> the scale drawing

x-----> the area of the playground in the scale drawing

y----> the area of the actual playground

`z^(2)=(x)/(y)`

we have

`x=16*8=128\ cm^(2)`

`y=72\ m^(2)`

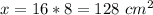
substitute

`z^(2)=(128)/(72)`

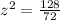
simplify

`z^(2)=(16)/(9)`

`z=(4)/(3)(cm)/(m)`

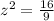
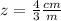
or

Divide by 4 both numerator and denominator

`z=(1)/(0.75)(cm)/(m)`