Question

The fill volume of an automated filling machine used for filling cans of carbonated beverage is normally distributed. Suppose, that the mean of the filling operation can be adjusted easily, but the standard deviation remains at 0.2 fluid ounce (a) At what value should the mean be set so that 99.9% of all cans exceed 10 fluid ounces? Round your answer to three decimal places (e.g. 98.765) fluid ounces (b) At what value should the mean be set so that 99.9% of all cans exceed 10 fluid ounces if the standard deviation can be reduced to 0.04 fluid ounce? Round your answer to three decimal places (e.g. 98.765) fluid ounces

Answer 1

a) 10.618; b) 10.124

Explanation:

For each of these, we use z scores. The formula for a z score is

`z=(X-\mu)/(\sigma)`

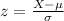
For both questions, we want the value of the mean, μ, that makes P(X > 10) = 0.999. However, the z table gives us the area to the left of a value, which is less than, not greater than. This means we want the value of μ that makes P(X ≤ 10) = 1-0.999 = 0.001.

Using a z table, we see that this value corresponds with a z score of -3.09.

For part a,

-3.09 = (10-μ)/0.2

Multiply each side by 0.2:

0.2(-3.09) = ((10-μ)/0.2)(0.2)

-0.618 = 10-μ

Subtract 10 from each side:

-0.618-10 = 10-μ-10

-10.618 = -μ

Divide both sides by -1:

-10.618/-1 = -μ/-1

10.618 = μ

For part b,

-3.09 = (10-μ)/0.04

Multiply both sides by 0.04:

0.04(-3.09) = ((10-μ)/0.04)(0.04)

-0.1236 = 10-μ

Subtract 10 from each side:

-0.1236-10 = 10-μ-10

-10.1236 = -μ

Divide both sides by -1:

-10.1236/-1 = -μ/-1

10.1236 = μ

10.124 ≈ μ