Question

Large stars can explode as they finish burning their nuclear fuel, causing a supernova. The explosion blows away the outer layers of the star. According to Newton's third law, the forces that push the outer layers away have reaction forces that are inwardly directed on the core of the star. These forces compress the core and can cause the core to undergo a gravitational collapse. The gravitational forces keep pulling all the matter together tighter and tighter, crushing atoms out of existence. Under these extreme conditions, a proton and an electron can be squeezed together to form a neutron. If the collapse is halted when the neutrons all come into contact with each other, the result is an object called a neutron star, an entire star consisting of solid nuclear matter. Many neutron stars rotate about their axis with a period of ≈ 1 s and, as they do so, send out a pulse of electromagnetic waves once a second. These stars were discovered in the 1960s and are called pulsars. (a) Consider a neutron star with a mass equal to the sun, a radius of 8 km, and a rotation period of 1.0 s. What is the speed of a point on the equator of the star? (b) What is g at the surface of this neutron star? (c) A stationary 1.2 kg mass has a weight on earth of 11.76 N. What would be its weight on the star? (d) How many revolutions per second are made by a satellite orbiting 1.4 km above the surface? (e) What is the radius of a geosynchronous orbit about the neutron star?

Answer 1

(a)
`5.02\cdot 10^4 m/s`

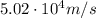
The radius of the neutron star is

R = 8 km = 8000 m

whole the rotation period is

T = 1.0 s

The speed of a point on the equator of the star will be given by the ratio between the circumference of the star (
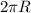`2\pi R`) and the time taken to complete one rotation (which is the period T):

`v=(2\pi R)/(T)=(2\pi(8000 m))/(1.0 s)=5.02\cdot 10^4 m/s`

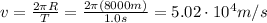
(b)
`2.07\cdot 10^(12)m/s^2`

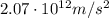
The value of the gravitational acceleration, G, at the surface of the star is given by

`g=(GM)/(R^2)`

where

G is the gravitational constant

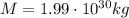`M=1.99\cdot 10^(30)kg` is the mass of the star (equal to the mass of the Sun)

R = 8000 m is the radius of the star

Solving the equation for g, we find

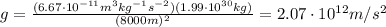
`g=((6.67\cdot 10^(-11)m^3 kg^(-1)s^(-2))(1.99\cdot 10^(30)kg))/((8000 m)^2)=2.07\cdot 10^(12)m/s^2`

(c)
`2.48\cdot 10^(12)N`

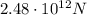
The object has a mass of

m = 1.2 kg

So its weight on the star will be given by

`W=mg`

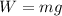
where m is the mass and
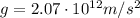`g=2.07\cdot 10^(12)m/s^2` is the acceleration due to gravity on the star. Solving the formula, we find

`W=(1.2 kg)(2.07\cdot 10^(12)m/s^2)=2.48\cdot 10^(12)N`

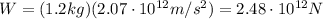
(d) 2012 rev/s

The gravitational attraction on the satellite is equal to the centripetal force that keeps it in orbit:

`(GMm)/((R+h)^2)=m\omega^2 (R+h)`

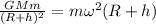
where

m = 1.2 kg is the mass of the satellite

R = 8000 m is the radius of the star

h = 1.4 km = 1400 m is the altitude of the satellite above the surface

`\omega` is the angular velocity of the satellite

Solving the equation for
`\omega`, we find

`\omega = \sqrt{(GM)/((R+h)^3)}=\sqrt{((6.67\cdot 10^(-11))(1.99\cdot 10^(30)kg))/((8000 m+1400 m)^3)}=12641 rad/s`

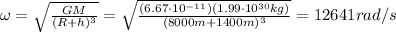
Converting into revolutions per second,

`\omega=(12641 rad)/(2\pi rad/rev)=2012 rev/s`

(e) 944 km

A geosynchronous orbit is an orbit whose period of revolution is equal to the period of rotation of the star:

`T'=T=1.0 s`

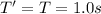
The speed of a satellite in orbit around the star is given by

`v=\sqrt{(GM)/(r)}`

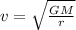
where r is the radius of the orbit.

Also, the orbital speed is given by the ratio between the circumference of the orbit and the period:

`v=(2\pi r)/(T)`

Putting the two equations together, we can find an expression for the orbital radius, r, as function of the period, T:

`\sqrt{(GM)/(r)}=(2\pi r)/(T)\\r=\sqrt[3]{(GM T^2)/(4\pi^2)}=\sqrt[3]{((6.67\cdot 10^(-11))(1.99\cdot 10^(30) kg)(1.0 s)^2)/((4\pi^2))}=9.44\cdot 10^5 m=944 km`