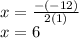Question

How many points does the given equation have in common with the x-axis and where is the vertex in relation to the x-axis. y=x^2-12x+12

Answer 1

1. It has two points in common with the x-axis.

2. The vertex in relation to the x-axis is at
`x=6`

Explanation:

The points that the equation has in common with the x-axis are the points of intersection of the parabola with the x-axis.

To find them, substitute y=0 and solve for "x":

`y=x^2-12x+12\\0=x^2-12x+12`

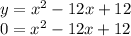
Use the Quadratic formula:

`x=(-b\±√(b^2-4ac))/(2a)\\\\x=(-(-12)\±√((-12)^2-4(1)(12)))/(2(1))\\\\x_1=10.89\\\\x_2=1.10`

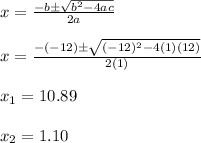
It has two points in common with the x-axis.

To find the vertex in relation to the x-axis, use the formula:

`x=(-b)/(2a)`

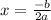
Substituting values, you get:

`x=(-(-12))/(2(1))\\x=6`