Question

A pendulum has 881 J of potential energy at the highest point of its swing. How much kinetic energy will it have at the bottom of its swing?

Answer 1

Hello!

The answer is: 881 J of kinetic energy.

Why?

The motion of a pendulum (with no friction considered) is a continuous exchange between potential energy and kinetic energy.

So, at the highest point of its swing, the potential energy will be the maximum potential energy that the pendulum can have and the kinetic energy will be 0 since at max height the speed tends to 0.

On the opposite side, when the pendulum is at the bottom (the lowest point of its swing) the potential energy will be the minimum (tends to 0) but the kinetic energy will be the maximum.

In the pendulum motion, the total energy is conserved, meaning that:

`PE_(h) +KE_(h)=PE_(l) +KE_(l)`

`PE=mgh\\KE=(1mv^(2) )/(2)`

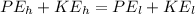
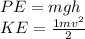
Where,

m is the mass of the object

g is the acceleration of gravity

h is the height

v is the speed

So, what is the energy at the bottom of its swing?

`881J +0=0 +881J\\881J=881J`

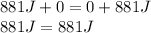
The energy is conserved.

So, the pendulum has 881J of kinetic energy at the bottom of its swing.