Question

The number of subscribers y to a newspaper after t years is shown by the equation below: y = 75(0.95)t Which conclusion is correct about the number of subscribers to the newspaper? It increased by 75% every year. It decreased by 75% every year. It increased by 5% every year. It decreased by 5% every year.

Answer 1

It decreased by 5% every year.

Explanation:

Given : The number of subscribers y to a newspaper after t years is shown by the equation below:
`y = 75(0.95)^t`

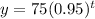
To Find: Which conclusion is correct about the number of subscribers to the newspaper?

Solution:

`y = 75(0.95)^t`

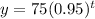
Initial amount of subscribers = 75

We can rewrite the given equation as
`y = 75(1-0.05)^t` ---A

General exponential decay function :
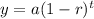`y=a(1-r)^t` --B

where y is the amount after t years

a is the initial amount

r is the rate of decrease in decimals

t is the time

If we compare A with B

So, rate of decrement = 0.05=5%

So, This shows that the number of subscribers decreased by 5% every year.

Hence Option D is correct.

It decreased by 5% every year.

Answer 2

It decreased by 5% every year

Explanation:

When t increases by 1, the number of subscribers is multiplied by another factor of 0.95, making the new value 5% less than the previous one.

The number of subscribers decreased by 5% every year.