Question

What is the area of the shaded portion of the circle

Answer 1

Answer: The correct option is (A)
`(16\pi-32)~\textup{in}^2.`

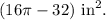
Step-by-step explanation: We are given to select the area of the shaded portion of the circle shown in the figure.

From the figure, wee that

there is a circle of radius, r = 8 in.

So, the area of the whole circle will be

`A_c=\pi r^2=\pi* 8^2=64\pi~\textup{in.}^2`

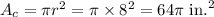
Now, the triangle shown is a right-angled one with base length 8 in and height 8 in.

So, the area of the triangle is given by

`A_t=(1)/(2)* 8*8=32~\textup{in.}^2`

Since the area of the shaded portion is equal to one fourth of the area of circle minus the area of the triangle, so we get

`Area~of~the~shaded~portion\\\\=(1)/(4)* A_c-A_t\\\\=(1)/(4)* 64\pi-32\\\\=(16\pi-32)~\textup{in}^2.`

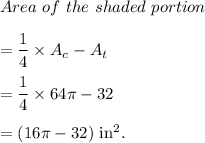
Thus, the required area of the shaded portion is
`(16\pi-32)~\textup{in}^2.`

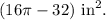
Option (A) is CORRECT.