Question

Please help! Worth 70 points!

Comparing Quadratic Functions


4. Two different quadratic functions have graphs with the same vertex. Which function’s graph increases faster between x = 2 and x = 3?


Function A


This is the picture attachment


Function B

x | y

–1 | 12.5

0 | 5

1 | 0.5

2 | –1

3 | 0.5

4 | 5

5 | 12.5


a. What is the vertex of each function's graph? (1 point)



b. What is the average rate of change in function A between x = 2 and x = 3? (2 points)



c. What is the average rate of change in function B between x = 2 and x = 3? (2 points)



d. Which function's graph increases faster between x = 2 and x = 3? (1 point)

Answer 1

4a. (2,-1)

4b. 1

4c. 1.5

4d. Function B

Explanation:

4a. The vertex of the function is the (x,y) point at the peak or valley of the parabola. In the picture, function A has its vertex at (2,-1). In the table, function B has its vertex at (2,-1) since the y values repeat around this part of the table.

4b-d. The average rate of change is the slope between the points at x = 2 and x = 3. Calculate the slope between points (2,-1) and (3,0) for Function A then for function B (2,-1) and (3,0.5).

`m = (y_2-y_1)/(x_2-x_1) = (0--1)/(3-2) = (1)/(1) = 1\\\\m = (y_2-y_1)/(x_2-x_1) = (0.5--1)/(3-2) = (1.5)/(1) = 1.5`

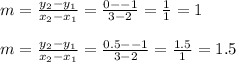
Function B has a greater average rate of change meaning it is increasing at a faster rate than Function A.