Answer:
Part 1)
Bob's mistake was to have used the cosine instead of the sine
The measure of the missing angle is
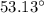
Part 2) The surface area of the pyramid is
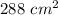
Explanation:
Part 1)
Let
x----> the missing angle
we know that
In the right triangle o the figure
The sine of angle x is equal to divide the opposite side angle x to the hypotenuse of the right triangle
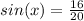

Bob's mistake was to have used the cosine instead of the sine
Part 2) we know that
The surface area of the square pyramid is equal to the area of the square base plus the area of its four lateral triangular faces
so
![SA=b^(2)+4[(1)/(2)(b)(h)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ca1dhz9vp0s8i6qe8d44q0vlil3buhleok.png)
where
b is the length side of the square
h is the height of the triangular lateral face
In this problem
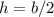 -------> by an 45° angle
-------> by an 45° angle
so
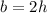
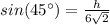
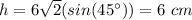
Find the value of b
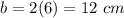
Find the surface area
![SA=12^(2)+4[(1)/(2)(12)(6)]=288\ cm^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/eoqeagrx5sqaj87qxgl1x40oqpmibaya1l.png)