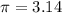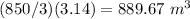Question

Find the volume of this composite solid

Answer 1

`889.67\ m^(3)`

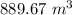
Explanation:

we know that

The volume of the composite solid is equal to the volume of the cylinder plus the volume of a cone

The volume of the cylinder is equal to

`V=\pi r^(2)h`

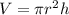
we have

`r=5\ m`

`h=10\ m`

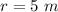
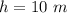
substitute

`V=\pi (5)^(2)(10)=250\pi\ m^(3)`

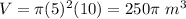
The volume of the cone is equal to

`V=(1/3)\pi r^(2)h`

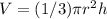
we have

`r=5\ m`

`h=4\ m`

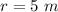
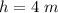
substitute

`V=(1/3)\pi (5)^(2)(4)=(100/3) \pi\ m^(3)`

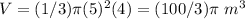
The volume of the composite solid is

`250\pi\ m^(3)+(100/3) \pi\ m^(3)=(850/3) \pi\ m^(3)`

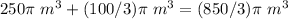
assume

`\pi=3.14`

`(850/3)(3.14)=889.67\ m^(3)`