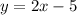Answer:
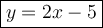
Explanation:
The slope-intercept form of an equation of a line:

Parallel lines have the same slope. Therefore if given line is
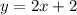
then the slope of our line is
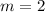 .
.
We have the equation:
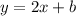
The line passes through (-1, -7). Put the coordinsted pf the point to the equation:
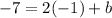
 add 2 to both sides
add 2 to both sides
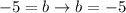
Finally: