Any line through the points
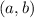 and
and
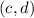 has
has
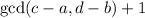
lattice points. In this case, the count is GCD(45, 264) + 1.
Using Euclid's algorithm, we have
264 = 5•45 + 39
45 = 1•39 + 6
39 = 6•6 + 3
6 = 2•3 + 0
so that GCD(45, 264) = 3. Then there are 3 + 1 = 4 lattice points.