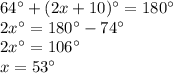Question

Given: circle k(O), ED diameter, m∠OEF=32°, m EF=(2x+10)°. Find: x

Answer 1

The value of x is
`53\°`

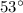
Explanation:

see the attached figure to better understand the problem

step 1

Find the measure of arc DF

we know that

The inscribed angle measures half that of the arc comprising

so

`m<OEF=(1)/(2)(arc\ DF)`

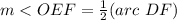
we have

`m<OEF=32\°`

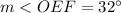
substitute

`32\°=(1)/(2)(arc\ DF)\\ arc\ DF=64\°`

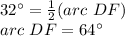
step 2

Find the measure of x

we know that

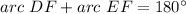`arc\ DF+arc\ EF=180\°` ---> is a semi circle

we have

`arc\ DF=64\°\\ arc\ EF=(2x+10)\°`

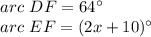
substitute

`64\°+(2x+10)\°=180\°\\ 2x\°=180\°-74\°\\ 2x\°=106\°\\ x=53\°`