ANSWER
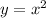
Step-by-step explanation
For a function to be an invertible, it must be a one-to-one function.
In other words , it's graph should pass the horizontal line test.
It is obvious that,
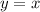
and
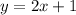
will pass the horizontal line test.
But
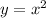
has a v-shape and hence cannot pass the horizontal line test.
This means that y=x² is not invertible. That is, its inverse is not a function.
Let us quickly check that:
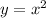
Interchange x and y.

Solve for y,
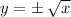
This is not a function, because it doesn't pass the vertical line test.