Answer:
The equation of parabola is:
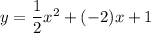
Explanation:
We know that the vertex form of the equation of parabola is given by:

where the vertex of the parabola is (h,k).
Now, from the graph i.e. provided to us we see that the vertex of the parabola is located at (2,-1)
i.e.
(h,k)=(2,-1)
i.e.
h=2 and k= -1
Hence, we have the equation of the parabola as:

Now, with the help of a passing through point of the parabola we may easily obtain the value of a.
The parabola passes through (0,1)
Hence, on putting x=0 and y=1 we have:
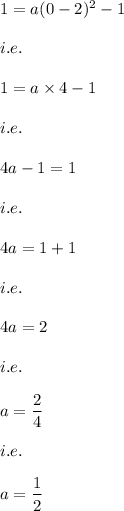
Hence, the equation of parabola will be:
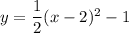
On expanding the square term we have:
