Question

7) T F If two forces of equal magnitude act on an object that is hinged at a pivot, the force acting farther from the pivot must produce the greater torque about the pivot.

Answer 1

False

Step-by-step explanation:

The torque exerted by a force is given by:

`\tau=Fd sin \theta`

where

F is the magnitude of the force

d is the distance between the point of application of the force and the pivot

`\theta` is the angle between the directions of F and d

We see that the magnitude of the torque depends on 3 factors. In this problem, we have 2 forces of equal magnitude (so, equal F). Moreover, one of the forces (let's call it force 1) acts farther from the pivot than force 2, so we have

`d_1 > d_2`

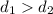
However, this does not mean that force 1 produces a greater torque. In fact, it also depends on the angle at which the force is applied. For instance, if the first force is applied parallel to d, then we have

`\theta_1 =0\\sin \theta=0`

and the torque produced by this force would be zero.

So, the statement is false.