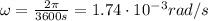Answer:
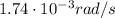
Step-by-step explanation:
The angular velocity of the hour hand is given by:
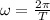
where
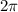 is the angular displacement (in radians) corresponding to one complete rotation
is the angular displacement (in radians) corresponding to one complete rotation
T is the period of the hour hand (the time it takes to complete one rotation)
The period of the hour hand is 1 hour, which is
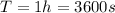
So the angular velocity is