Answer:
Second Option: 3, -3
Explanation:
In the graph of the supplied function we observe f (x) is a piece wise function composed of two line segments and a point.
 if
if
 ,
,
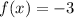 if
if
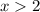 ,
,
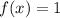 if
if
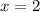
We must find the limit when x approaches 2 from the left
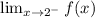
and we must find the limit when x approaches 2 on the right.

when x approaches 2 on the left then
 . If
. If
 then
then
 , therefore the
, therefore the
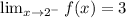
When x approaches 2 on the right then
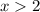 . If
. If
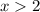 then
then
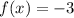 , therefore the
, therefore the
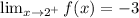 .
.