Answer:
1) 46%
2) 0.07
3) 0.1148
4) 0.1372
Explanation:
Total number of patients = 50
Total number of dogs = 7 + 4 + 5 + 5 + 2 = 23
Part 1)
The percentage of patients that were dogs =
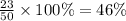
Thus, 46% of the patients were dogs.
So,
p =46% = 0.46
Part 2)
p = 0.46
n = 50
Using the values in the given formula, we get:
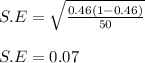
Thus, the standard error is 0.07
Part 3)
Z-value for 90% confidence interval is 1.64. This value is found using z-table or can be found using online calculators.
Margin of error = z-value x S.E
Using the values, we can write:
Margin of error = 1.64 x 0.07
Margin of error = 0.1148
Thus margin of error for 90% confidence interval is 0.1148
Part 4)
Z-value for 95% confidence interval is 1.96
Margin of error = z-value x S.E
Using the values, we can write:
Margin of error = 1.96 x 0.07
Margin of error= 0.1372
Thus margin of error for 95% confidence interval is 0.1372