(a) 1.98 m/s
Due to the law of conservation of energy, the initial kinetic energy of the flea will be equal to its gravitational potential energy when it reaches the highest position in the jump:
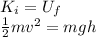
where
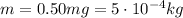 is the mass of the flea
is the mass of the flea
v is the take-off speed
g = 9.81 m/s^2 is the gravitational acceleration
 is the maximum height reached by the flea
is the maximum height reached by the flea
Solving the formula for v, we find

(b)
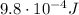 , 1.96 J/kg
, 1.96 J/kg
The kinetic energy of the flea at take off is given by

where
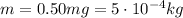
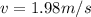
Substituting,
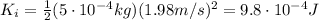
While the kinetic energy per kilogram of mass is
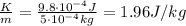
(c) 200 m, 62.6 m/s
The flea jumps 0.20 m having a length of 2.0 mm = 0.002 m. The man has a length of 2.0 m, so in proportion he would jump at a maximum height of

And he should have a takeoff speed of

(d) 5.88 J/kg
Most humans can jump to a maximum height of
h = 60 cm = 0.60 m
so the take off speed is

So, its kinetic energy per kilogram of mass would be:
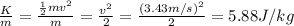
(e) In the chemical and elastic potential energy store
The flea stores the energy that allows it to make the leap as chemical potential energy and elastic potential energy of its muscles, that are stretched and allows it to make the big jump.