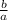Answer:
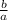
Explanation:
A variable raised to a negative exponent p is equivalent to 1 divided by the variable raised to a positive exponent p.
In this equation, this rule applies to both b variables as follows:
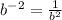
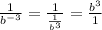
After 'solving' for each negative exponent, you can plug them into the previous negative exponents:
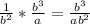
Afterwards, cancel out b^2 from the top and bottom of the equation to get your final answer, as b^2 / b^2 = 1