Question

Can someone help me with #18 & #20?​

Answer 1

`\large\boxed{18)\ x=13\ and\ y=9}\\\boxed{20)\ AO=8}`

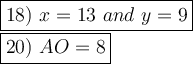
Explanation:

18)

If a quadrilateral is inscribed in a circle, the opposite angles add up to 180°.

Therefore we have the system of equations:

`\left\{\begin{array}{ccc}(6x+23)+(8y+7)=180\\(6x-4)+(12y-2)=180\end{array}\right\\\\\left\{\begin{array}{ccc}6x+8y+(23+7)=180\\6x+12y+(-4-2)=180\end{array}\right\\\left\{\begin{array}{ccc}6x+8y+30=180&|\text{subtract 30 from both sides}\\6x+12y-6=180&|\text{add 6 to both sides}\end{array}\right\\\left\{\begin{array}{ccc}6x+8y=150\\6x+12y=186&|\text{multiply both sides by (-1)}\end{array}\right`

`\underline{+\\\left\{\begin{array}{ccc}6x+8y=150\\-6x-12y=-186\end{array}\right}\qquad\text{add both sides of the equations}\\.\qquad\qquad-4y=-36\qquad|\text{divide both sides by (-4)}\\.\qquad\qquad\boxed{y=9}\\\\\text{Put the value of y to the first equation and solve them for x:}\\\\6x+8(9)=150\\6x+72=150\qquad\text{subtract 72 from both sides}\\6x=78\qquad\text{divide both sides by 6}\\\boxed{x=13}`

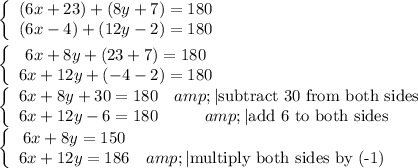
20)

If line AB is tangent to the circle, then the angle A is a right angle

`m\angle A=90^o`

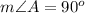
Therefore the triangle is a right triangle. We can use the Pythagorean theorem:

Let O - center of the circle. Therefoe OA is the radius of a circle.

From a Pythagorean theorem:

`AO^2+15^2=(9+8)^2\\\\AO^2+225=17^2\\\\AO^2+225=289\qquad\text{subtract 225 from both sides}\\\\AO^2=64\to AO=√(64)\\\\AO=8`