Question

What is the sum of an infinite geometric series if 2=5 and r=1/3

Answer 1

`(15)/(2)`

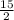
Explanation:

The problem has a mistake, it should NOT be 2 = 5, rather a=5.

Now, given a = 5 (the first term is a), and

r = 1/3 (common ratio),

we can solve for the sum of the infinite series by using the formula:

`S_(\infty)=(a)/(1-r)`

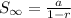
Where
`S_(\infty)` is the sum of the infinite geometric series,

a is the first term (given as 5), and

r is the common ratio ( r= 1/3 given)

We now plug these into the formula and get our answer:

`S_(\infty)=(a)/(1-r)\\=(5)/(1-(1)/(3))\\=(5)/((2)/(3))\\=(15)/(2)`