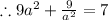Question

asked Sep 24, 2020 163k views

2 Answers

Martin Stone · Answer 1 · 2020-09-25T07:03:59+0000

Answer:

The value for the given expression:

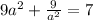
9 a^(2)+(9)/(a^(2))=7

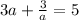
3 a+(3)/(a)=5

First, we need to square both the sides of the given expression:

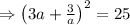
$\Rightarrow\left(3 a+(3)/(a)\right)^(2)=25$

On applying the below algebraic identity:

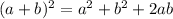
(a+b)^(2)=a^(2)+b^(2)+2 a b

We get,

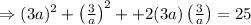
$\Rightarrow(3 a)^(2)+\left((3)/(a)\right)^(2)++2(3 a)\left((3)/(a)\right)=25$

On squaring the terms:

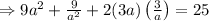
$\Rightarrow 9 a^(2)+(9)/(a^(2))+2(3 a)\left((3)/(a)\right)=25$

On cancelling the ‘a’ variable:

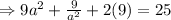
$\Rightarrow 9 a^(2)+(9)/(a^(2))+2(9)=25$

On multiplying the constants:

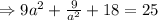
$\Rightarrow 9 a^(2)+(9)/(a^(2))+18=25$

On taking constant on one side and keeping variable on one side:

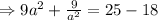
$\Rightarrow 9 a^(2)+(9)/(a^(2))=25-18$

On subtracting the constants, we get the final answer as:

$\therefore 9 a^(2)+(9)/(a^(2))=7$

Eudes · Answer 2 · 2020-10-01T08:33:31+0000

Answer:

7

Explanation:

Squaring the first equation gives ...

9a^2 + 2·3a·3/a + 9/a^2 = 25

The factors of "a" in the middle term cancel, leaving ...

9a^2 +9/a^2 +18 = 25

Subtracting 18 answers the question:

9a^2 +9/a^2 = 7