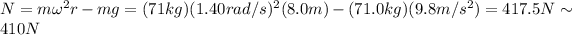Answer:
410 N
Step-by-step explanation:
At the highest point, there are two forces pushing the man towards the centre of the cylinder: the normal reaction (N) and his weight (W=mg). The sum of these two forces must be equal to the centripetal force. So we have
 (1)
(1)
where
m = 71 kg is the mass of the rider
g = 9.8 m/s^2
r = 8.0 m is the radius of the cylinder
 is the angular frequency
is the angular frequency
The cylinder rotates once every 4.5 s (period), so its angular frequency is

So by solving eq.(1) for N, we find the force with which the wall pushes the rider: