Question

Use the elimination method to solve the system of equations . Choose the correct ordered pair -3y = x - 5 x + 5y = 7

Answer 1

`(2,1)`.

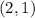Explanation:

We have been given a system of equations. We are asked to solve our given system using elimination method.

`-3y=x-5...(1)`

`x+5y=7...(2)`

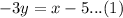
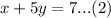
First of all, we will gather all terms of both equations on left side as shown below:

`-x-3y+5=0...(1)`

`x+5y-7=0...(2)`

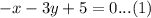
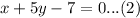
Adding equation (1) and (2), we will get:

`-x+x-3y+5y+5-7=0\rightarrow 2y-2=0`

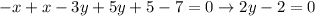
Now, we will add 2 on both sides of our equation as shown below:

`2y-2+2=0+2`

`2y=2`

`(2y)/(2)=(2)/(2)`

`y=1`

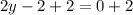
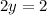
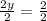
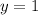
Upon substituting
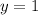`y=1` in equation (2), we will get:

`x+5*1=7`

`x+5=7`

`x=7-5`

`x=2`

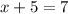
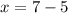
Therefore, the solution for our given system of equations would be
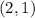`(2,1)`.