Answer:
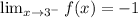
Explanation:
We have a piesewise function composed of three pieces. two line segments and one point.
The first line cuts at point (0,0) and ends at point (3, -1)
If we use these two points we can find the equation of the line.
The slope m is:
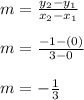
So the equation is:
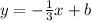
As the line cuts in (0,0) then
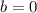 and the equation is:
and the equation is:
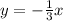
The equation of the second line is:
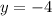
Now we can find f(x) (although it is not necessary to find the equation of f(x) because we have its graph)
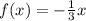 if
if
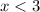 ;
;
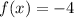 if
if
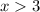 ;
;
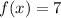 if
if
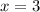 .
.
The limit of f(x) when x tends to 3 from the left
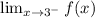 is the limit of the function when x approaches 3 from the left. If x approaches 3 from the left then
is the limit of the function when x approaches 3 from the left. If x approaches 3 from the left then
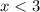 . If
. If
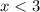 then f(x) is given by the line
then f(x) is given by the line
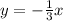 . Then the limit is -1 as seen in the graph
. Then the limit is -1 as seen in the graph