Question

URGENT!!! Jean needs to cut a triangular piece of tile for a mosaic. In order to cut it properly, she needs to know the measure of the unknown angle ?∘ as shown in the figure. The lengths of PQ, QR, and PR are 90 millimeters, 77 millimeters, and 151 millimeters respectively. What is the value of the unknown angle?

Select the correct answer below:

23

27

39

50

51

Answer 1

50.74 degrees

Explanation:

To find the value of the unknown angle, we have to find the value of the angle RQP.

Since we have the lengths of the 3 sides, it's easy with the Cosines Law, that says:

`cos(A) = (b^(2) + c^(2) - a^(2))/(2 * b * c)`

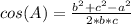
So, let's say a = 151, b = 77 and c = 90

If we isolate A, which is our Q in the figure, we get:

`A = cos^(-1) ((b^(2) + c^(2)  - a^(2) )/(2 * b * c) ) = cos^(-1) ((77^(2) + 90^(2) - 151^(2) )/(2 * 77 * 90) ) = 129.26`

We now know that angle RQP is 129.26 degrees.

Since the line PQ is extended... we know this forms a 180 degree flat angle. If we then subtract the 129.26 degrees from the 180 angle, we get 50.74 degrees.