Question

A town has a population of 20000 and grows at 4% every year. How long will it be until the population will reach 39400?

Answer 1

The population will be 39400 in approximately 17 years

Explanation:

The increase in population after t years is given by the formula

`P_t = P_0(1+r)^t`

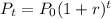
Here

P_0 is the initial population

r is the growth rate and t is time in years

So far we know,

P_0 = 20000

r = 4%

P_t = 39400

Putting the values in the formula

`39400 = 20000(1+0.04)^t\\39400 =20000(1.04)^t\\(39400)/(20000) = (1.04)^t\\1.97 = (1.04)^t`

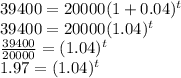
Taking natural log on both sides

`ln |(1.04)^t| = ln |1.97|\\t\ ln\ |1.04| = ln\ |1.97|\\t = (ln\ 1.97)/(ln\ 1.04)\\t = 17.287\\t \approx 17`

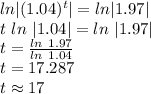
Hence,

The population will be 39400 in approximately 17 years