Question

3. A salesperson makes a base salary of $2100 per month. Once he reaches $42000 in total sales, he earns an additional 5% comission on the amount of sales over $42000.

a. (2 points) Write a piecewise-defined function to model the salesperson’s total monthly salary S(x) (indollars) as a function of the amount of sales x.

b. (2 points) Graph the function. Indicate the numerical scale on the horizontal and vertical axes of
your graph, and indicate which axis represents the salary and which is the sales.

c. (1 point) If the salesperson had $80000 in sales, how much was his salary for that month?

d. (2 points) If the salesperson’s total salary for a month was $4500, how much were his total sales for
that month?

e. (2 points) Compute S(25000) and interpret what this means in the context of the problem (in terms of
the monthly salary and the sales)

Answer 1

a) The salesperson’s total monthly salary
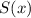`S(x)` as a function of the amount of sales (x) can be modeled by the following piecewise-defined function:

`[S(x) = \begin{cases} $2100 & \text{if } x \leq $42000, \ $2100 + 0.05(x - $42000) & \text{if } x > $42000. \end{cases}]`

b) The graph would be a horizontal line at
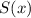`S(x)`= $2100) for
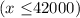`(x \leq $42000)`, and a line with a positive slope for (x > $42000), starting at the point (($42000, $2100)). The slope of this line would be 0.05, representing the 5% commission rate.

c) If the salesperson had $80000 in sales, his salary for the month was $4,000.

d) If the salesperson’s total salary for a month was $4500, his total sales for that month was $90,000.

e. S(25,000) shows that the salesperson earned a salary of $25,000 for the month. The salesperson recorded a sales of $500,000 for the month to earn this salary.

The base salary of the salesperson per month = $2,100

The total sales expected before earning an additional commission = $42,000

Sales Commission = 5% of Sales over $42,000

a) This piecewise-defined function says that the salesperson makes a base salary of $2100 per month if his sales are $42000 or less. If his sales exceed $42000, he makes his base salary plus an additional 5% commission on the amount of sales over $42000.

b. The x-axis would represent the amount of sales (x), and the y-axis would represent the salary
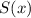`S(x)`. The graph is a horizontal line starting at
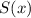`S(x)`= $2100) for
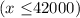`(x \leq $42000)`, and a line with a positive slope for (x > $42000), starting at the point (($42000, $2100)). The slope of this line would be 0.05, representing the 5% commission rate. The numerical scale on the axes would depend on the range of sales and salary values.

c. The salesperson's sales for the month = $80,000

Salary for the month = $2,100 + [($80,000 - $42,000) x 5%]

= $2,100 + $1,900

= $4,000

d. The salesperson's salary for a month = $4,500

Base salary = $2,100

Commission = $2,400 ($4,500 - $2,100)

Total sales for the month = $90,000 [$42,000 + ($2,400/0.05)]

e. S(25,000) = Salary of $25,000 for the month:

Base salary = $2,100

Commission $22,900 ($25,000 - $2,100)

Total sales for the month = $500,000 [$42,000 + ($22,900/0.05)]

Answer 2

The piecewise-defined function to model the salesperson's total monthly salary (in $) is,

f(x)=\begin{cases}2000 & \text{ if } x\leq 40,000 \\2000+0.05(x-40000) & \text{ if } x>40000\end{cases}

Step-by-step explanation:It is given that the salesperson makes a base salary of $2000 a month. Once he reaches $40,000 in total sales, he earns an additional 5% commission on the amount in sales over $40,000.

Let the x represents the amount of sales and f(x) represents the salary of salesperson.

It means till the sale of $40,000, the salary of the salesperson is constant, i.e., $2000.

for

He will get commision of 5% on the amount in sales over $40,000.

for

Therefore the piecewise-defined function to model the salesperson's total monthly salary (in $) is,