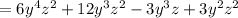Question

Find the product.

3y 2 z(2y 2 z + 4yz - y + z)

A 4y 6z 2 + 13y 3z 12 - 3y 2z 2 - 3yz

B 6y 4z 2 + 12y 3z 2 - 3y 3z + 3y 2z 2

C 6y 2z 4 - 12y 2z 3 + 3yz 3 - 3y 2z 2

D 3y 4z 2 + 3y 3z 2 - 6y 3z - 4

Answer 1

Answer :


`6{y}^(4) {z}^(2) + 12 {y}^(3) {z}^(2)-3 {y}^(3) {z}+3 {y}^(2) {z}^(2)`

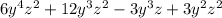
Step-by-step explanation :

To find the product of


`3 {y}^(2) z(2 {y}^(2) z + 4yz - y + z)`

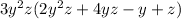
First we expand the bracket ,

it implies that, we use the expression outside the bracket to multiply individual expressions inside the bracket.

Hence


`3 {y}^(2) z(2 {y}^(2) z + 4yz - y + z)`


`= 3 {y}^(2) z(2 {y}^(2) z) + 3 {y}^(2) z(4yz) - 3 {y}^(2) z(y )+3 {y}^(2) z( z)`

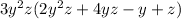
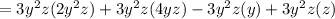
we now apply the law of indices


`{a}^(m) * {a}^(n) = {a}^(m+n)`

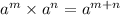
meaning, when you are multiplying two expressions with the same bases , repeat one of the bases and add the exponents.

Then, simplify to obtain


`= 6{y}^(4) {z}^(2) + 12 {y}^(3) {z}^(2)-3{y}^(3) {z}+3 {y}^(2) {z}^(2)`