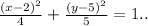Answer:
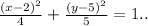
Explanation:
Major axis is the line joining the vertices A(2, 3) and A'(2, 7), x = 2..
The axes of the hyperbola are parallel to the axes of coordinates.
Distance between vertices AA' = major-axis length = 2 a = 4. a = 2..
The center C is the midpoint of AA'. So, C is (2, 5)
The distance between foci S(2, 2) and S'(2, 8), SS' = 2 a (eccentricity) = 2 a e = 6.
So,
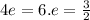
The semi-transverse axis is
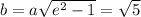
The equation required is the equation of the hyperbola with center at C(2, 5), axes parallel to axes of coordinates and semi-axes
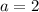 and
and
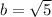 is....
is....