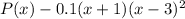Question

How do I solve this? I attached a screenshot

Answer 1

`P(x) -0.1(x+1)(x-3)^2`

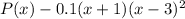
Explanation:

So you can express a polynomial in factored form, where each factor of the polynomial is being multiplied by each other to get the original polynomial as such:
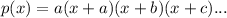`p(x) = a(x+a)(x+b)(x+c)...` notice the a in front? Sometimes the value is 1, sometimes it's not, and I'm assuming it's not 1, since the y-intercept is given.

Anyways, when we express a polynomial in factored form:
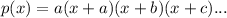`p(x) = a(x+a)(x+b)(x+c)...`, it's pretty easy to see that -a, -b, and -c are roots, since if we plug in -a, the factor (x+a) becomes (-a + a) = 0, and since the factors are being multiplied by each other, the value p(-a) will be 0, since 0 * some value = 0.

The next thing to know is what multiplicity means. It essentially means when you have the same root "multiple times", or in other words it's the degree of the factor. For example:
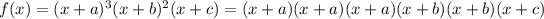`f(x) = (x+a)^3(x+b)^2(x+c) = (x+a)(x+a)(x+a)(x+b)(x+b)(x+c)`, if you took each factor, you would see that the root -a shows up 3 times, thus the multiplicity is 3, which can also be determined by just looking at the initial degree... 3. The same thing goes for b and c, except for c, the degree isn't explicitly said, it's just 1.

Since we have a zero at x=3 one of the factors will be (x-3) since plugging in 3 to this makes it 0. But this has a multiplicity of 2, so the degree of the this factor is 2. So for we have the polynomial:
`p(x) = (x-3)^2`

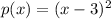
Since we have a zero at x=-1, one of the factors will be at (x+1), since plugging in 1 into this makes the value 0. This has a multiplicity of 1, and you can write the degree 1, but if you don't explicitly write it, it can just be assumed to be 1, since a^1=a

So now we have the polynomial:
`p(x) = (x+1)(x-3)^2`

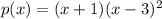
So let's just assume we have an "a" value in front as mentioned in the very beginning, we have the polynomial:
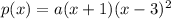`p(x) = a(x+1)(x-3)^2` and we can solve for this value, using any point except for the zeroes. We can use the y-intercept given to solve for a

Plug in 0 as x (by definition of y-intercept) and set p(x) = -0.9

`-0.9 = a(0+1)(0-3)^2`

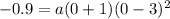
Subtract/add values

`-0.9 = a(1)(-3)^2`

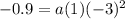
Simplify

`-0.9 = 9a`

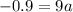
Divide both sides by 9

-0.1 = a

So now let's plug this into our polynomial to get the final result!

`P(x) -0.1(x+1)(x-3)^2`