Question

.Write the vertex and indicate if the graph opens up or down. y = 2x2 + 8x + 3

A. (2,5) down
B. (-2,5) up
C. (-2,-5) down
D. (-2,-5) up​

Answer 1

Given:

The equation of the parabola is

`y=2x^2+8x+3`

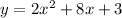
To find:

The vertex and check whether it opens up or down.

Solution:

We have,

`y=2x^2+8x+3`

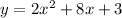
Here, leading coefficient is 2 which is a positive number. So, the parabola opens up.

The vertex of parabola
`f(x)=ax^2+bx+c` is

`\left((-b)/(2a),f((-b)/(2a))\right)`

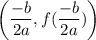
Here, a=2, b=8 and c=3.

`(-b)/(2a)=(-8)/(2(2))`

`(-b)/(2a)=(-8)/(4)`

`(-b)/(2a)=-2`

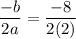
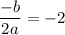
Putting x=-2 in the given equation.

`y=2(-2)^2+8(-2)+3`

`y=2(4)+(-16)+3`

`y=8-16+3`

`y=-5`

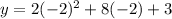
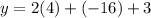
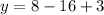
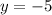
So, the vertex of the parabola is at (-2,-5) and parabola opens up.

Therefore, the correct option is D.