Question

A ray of light traveling in air is incident on the surface of a block of clear ice (of index 1.309) at an angle of 25.5 ◦ with the normal. part of the light is reflected and part is refracted. find the angle between the reflected and the refracted light. answer in units of ◦ .

Answer 1

Answer:
`135.29\º`

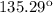
The figure attached will be helpful to understand the solution.

Here we see two cases, reflection and refraction of light.

According to the laws of reflection:

1. The incident ray, the reflected ray and the normal are in the same plane.

2. The angle of incidence is equal to the angle of reflection.

*Note the normal is perpendicular to the plane, with a
`90\º` angle with the surface

And this can be visualized in the figure, where the angle
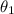`{\theta}_(1)` with which the incident ray hits the surface is equal to the angle with which this same ray is reflected.

On the other hand we have Refraction, a phenomenon in which the light bends or changes its direction when passing through a medium with a refractive index different from the other medium.

In this context, the Refractive index is a number that describes how fast light propagates through a medium or material.

According to Snell’s Law:

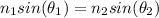`n_(1)sin(\theta_(1))=n_(2)sin(\theta_(2))` (1)

Where:

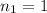`n_(1)=1` is the first medium refractive index (the air)

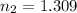`n_(2)=1.309` is the second medium refractive index (the ice)

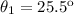`\theta_(1)=25.5\º` is the angle of the incident ray

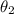`\theta_(2)` is the angle of the refracted ray

Now, firstly we have to find
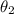`\theta_(2)` and then, by geometry, find
`\alpha` and
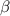`\beta` which sum the angle between the reflected and the refracted light.

Finding
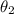`\theta_(2)` from (1):

`(1)sin(25.5\º)=(1.309)sin(\theta_(2))`

`sin(\theta_(2))=0.328`

`\theta_(2)=arcsin(0.328)`

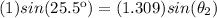
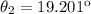`\theta_(2)=19.201\º` (2)

Remembering that the Normal makes a
`90\º` angle with the surface, we can say:

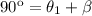`90\º=\theta_(1)+\beta` (3)

Finding
`\beta`:

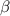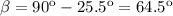`\beta=90\º-25.5\º=64.5\º` (4)

Doing the same with
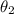`\theta_(2)` and
`\alpha}`:

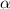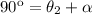`90\º=\theta_(2)+\alpha` (5)

Finding
`\alpha`:

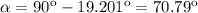`\alpha=90\º-19.201\º=70.79\º` (6)

Adding both angles (4) and (6):

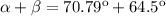`\alpha+\beta=70.79\º+64.5\º` (7)

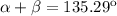`\alpha+\beta=135.29\º`>>>This is the angle between the reflected and the refracted light.