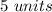Question

asked Dec 5, 2020 164k views

2 Answers

Benilda Key · Answer 1 · 2020-12-10T09:09:48+0000

Answer:

The length of shortest side is
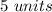
$5\ units$

Explanation:

Let

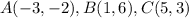
A(-3,-2),B(1,6),C(5,3)

we know that

the formula to calculate the distance between two points is equal to

$d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}$

step 1

Find the distance AB

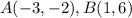
A(-3,-2),B(1,6)

substitute in the formula

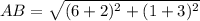
$AB=\sqrt{(6+2)^(2)+(1+3)^(2)}$

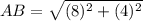
$AB=\sqrt{(8)^(2)+(4)^(2)}$

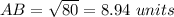
$AB=√(80)=8.94\ units$

step 2

Find the distance BC

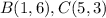
B(1,6),C(5,3)

substitute in the formula

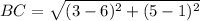
$BC=\sqrt{(3-6)^(2)+(5-1)^(2)}$

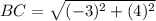
$BC=\sqrt{(-3)^(2)+(4)^(2)}$

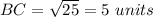
$BC=√(25)=5\ units$

step 3

Find the distance AC

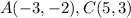
A(-3,-2),C(5,3)

substitute in the formula

$AC=\sqrt{(3+2)^(2)+(5+3)^(2)}$

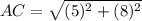
$AC=\sqrt{(5)^(2)+(8)^(2)}$

$AC=√(89)=9.43\ units$

Compare the length sides

The length of shortest side is
$5\ units$

Please log in or register to add a comment.