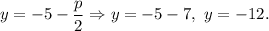Answer:
Vertex - (4,-5)
Focus (4,2)
Directrix y=-12
Explanation:
The equation
 of the parabola shows that its vertex is at point (4,-5). Multiply the equation by 28:
of the parabola shows that its vertex is at point (4,-5). Multiply the equation by 28:
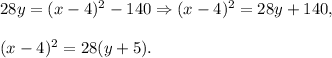
The parameter p of the parabola is
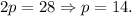
The coordinates of the focus will be
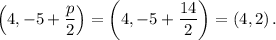
The directrix has the equation