Question

The graph h = −16t^2 + 25t + 15 models the height and time of a ball that was thrown off of a building where h is the height in feet and t is the time in seconds. At about what time did the ball reach the maximum height?

A) 0.80 seconds
B) 1 second
C) 2 seconds
D) 15 seconds

Answer 1

A

Explanation:

If you graph the equation f(x) = -16x^2+25x+15. You would need to pay attention to the x value which is somewhere in between 0.75-0.9.

Another way is to convert the equation into vertex form.

Answer 2

Option A.

Explanation:

The given function is

`h=-16t^2+25t+15`

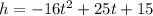
It models the height and time of a ball that was thrown off of a building where h is the height in feet and t is the time in seconds.

If a parabola is defined by function
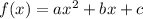`f(x)=ax^2+bx+c`, then the vertex of the parabola is

`Vertex=(-(b)/(2a),f(-(b)/(2a)))`

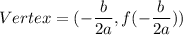
In the given function a=-16, b=25 and c=15. It is a downward parabola and vertex of a downward parabola is point of maximum.

We need to find the time at which the height of ball is maximum. It means we need to find the x-coordinate of the vertex.

`-(b)/(2a)=-(25)/(2(-16))=0.78125\approx 0.80`

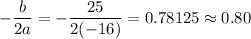
It means the ball reach the maximum height at about 0.80 seconds.

Therefore, the correct option is A.