Question

What is that answer to this question?

Answer 1

Answer:
`cos(F)=(5)/(13)`

Explanation:

The trigonometric identity needed to answer this question is:

`cos\alpha=(adjacent)/(hypotenuse)`

Therefore:

Indentify the angle, the opposite side and the adjacent side of the right triangle from the figure:

`adjacent=5\\hypotenuse=13\\\alpha=F`

Substitute them into
`cos\alpha=(adjacent)/(hypotenuse)`, then we get:

`cos(F)=(5)/(13)`

Answer 2

5/13

Explanation:

Cosine ratio for an angle is defined as the ratio of Adjacent side to Hypotenuse.

We have to find the cosine ratio for angle F. The side adjacent to angle F is side GF and the hypotenuse of the triangle is side FH. The side opposite to the right angle is always the hypotenuse.

So, we can write:

`\textrm{Cosine Ratio}=(Adjacent)/(Hypotenuse)\\\\ \textrm{Cosine Ratio of F}=(FG)/(FH) \\\\ \textrm{Cosine Ratio of F}=(5)/(13)`

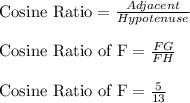
Therefore, the cosine ratio of angle F is 5/13