ANSWER
The given trinomial will have two distinct real solutionss.
EXPLANATION
The given trinomial is
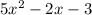
When we compare to
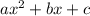
, we have a=5, b=-2, c=-3
The discriminant of a quadratic trinomial helps us to predict the nature of the roots of a quadratic trinomial without necessarily solving for them.
We now use the discriminant
D=b²-4ac
to obtain,
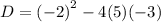
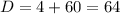
Since the discriminant is positive, the trinomial will have two distinct real solutions.