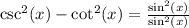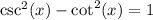Question

How can csc^2-cot^2 = 1?

Answer 1

By simplifying the left hand side using the Pythagorean Identity.

Step-by-step explanation

The given identity is

`\csc^(2) (x) - \cot^(2) (x) = 1`

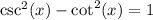
Take the left hand side and simplify to get the right hand side.

`\csc^(2) (x) - \cot^(2) (x) = (1)/(\sin^(2) (x)) - ( \cos^(2) (x))/(\sin^(2) (x))`

Collect LCM for the denominators.

`\csc^(2) (x) - \cot^(2) (x) = (1 - \cos^(2) (x))/(\sin^(2) (x))`

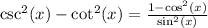
Recall the Pythagorean Identity.

`\cos^(2) (x) + \sin^(2) (x) = 1`

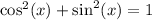
This implies that:

`1 - \cos^(2) (x) = \sin^(2) (x)`

We substitute this to get,

`\csc^(2) (x) - \cot^(2) (x) = (\sin^(2) (x))/(\sin^(2) (x))`

`\csc^(2) (x) - \cot^(2) (x) = 1`