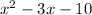Question

The answer is a, but please explain how you got the answer.

Answer 1

You can see that the function crosses the x axis at x= -2 and x=5.

With this knowledge, we can justify the answer in more than one ways. For example, a polynomial with such roots is

`(x+2)(x-5) = x^2-3x-10`

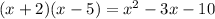
Alternatively, we know that in a quadratic equation in the form

`x^2-sx+p`

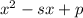
s is the sum of the roots and p is their product. In our case, the sum is 3 and the product is -10, so again we come to the conclusion that the equation is

`x^2-3x-10`