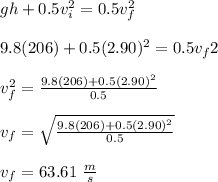Question

The beautiful Multnomah Falls in Oregon are approximately 206m high. If the Columbia river is flowing horizontally at 2.90m/s just before going over the falls, what is the overall velocity of the water when it hits the bottom?

Answer 1

The overall velocity of the water when it hits the bottom is:

`v_f=63.61\ (m)/(s)`

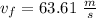
Step-by-step explanation:

Use the law of conservation of energy.

Call it instant [1] to the moment when the water is just before reaching the falls.

At this moment its height h is 206 meters and its velocity horizontally
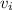`v_i` is
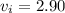`v_i = 2.90`m/s.

At the instant [1] the water has gravitational power energy
`E_g`

`E_g = mgh`

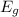
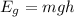
The water also has kinetic energy Ek.

`E_k = 0.5mv_i ^ 2`

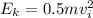
Then the Total E1 energy is:

`E_1 = mgh + 0.5mv_i ^ 2`

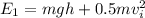
In the instant [2] the water is within an instant of touching the ground. At this point it only has kinetic energy, since the height h = 0. However at time [2] the water has maximum final velocity
`v_f`

So:

`E_2 = 0.5mv_f ^ 2`

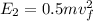
As the energy is conserved then
`E_1 = E_2`

`mgh + 0.5mv_i ^ 2 = 0.5mv_f ^ 2`

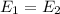
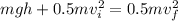
Now we solve for
`v_f`.

`gh + 0.5v_i ^ 2 = 0.5v_f ^ 2\\\\9.8(206) + 0.5(2.90) ^ 2 = 0.5v_f 2\\\\v_f^2 = (9.8(206) + 0.5(2.90) ^ 2)/(0.5)\\\\v_f = \sqrt{(9.8(206) + 0.5(2.90) ^ 2)/(0.5)}\\\\v_f=63.61\ (m)/(s)`