Question

On the Apollo 14 mission to the moon, astronaut Alan Shepard hit a golf ball. The acceleration due to gravity on the moon is 1/6 of its value on the earth (gravity on moon -1.633m/s2 ). On earth, golf balls are driven at about 84 m/s with a loft angle of about 15º and have a range of about 353 meters. Given the same initial speed and loft angle as on the earth, what was (a) the time of flight for the golf ball and (b) what was the range on the moon?

Answer 1

Answers:

This is a parabolic movement, this means it has an X-component and Y-component, and is described by the following equations:

For the Velocity:

`V_(o)=V_(ox)+V_(oy)`

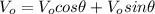`V_(o)=V_(o)cos\theta+V_(o)sin\theta` (1)

Where
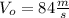`V_(o)=84(m)/(s)` is the initial Velocity and
`\theta=15\º`

`V=V_(ox)+V_(oy)+gt`

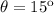
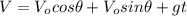`V=V_(o)cos\theta+V_(o)sin\theta+gt` (2)

Where
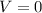`V=0` is the final Velocity, which in this case is zero and
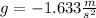`g=-1.633(m)/(s^(2))` is the acceleration due gravity in the moon.

For the distance
`r`:

`r=V_(ox)t+x_(o)+(1)/(2)gt^(2)+V_(oy)+y_(o)`

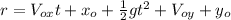
Where
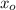`x_(o)` and
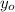`y_(o)` are the components of the initial position of the ball and we will assume it as zero in our reference system.

Therefore the equation for distance becomes:

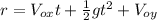`r=V_(ox)t+(1)/(2)gt^(2)+V_(oy)` (3)

And can be written as:

`r=V_(o)cos\theta.t+(1)/(2)gt^(2)+V_(o)sin\theta`

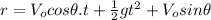
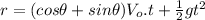`r=(cos\theta+sin\theta)V_(o).t+(1)/(2)gt^(2)` (4)

Having this established, let's begin with the answers:

(a) The time of flight for the golf ball

For this case, the equation of the velocity will be useful (equation 2):

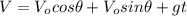`V=V_(o)cos\theta+V_(o)sin\theta+gt` (5)

Substituting the known values and solving to find
`t`

`0=84(m)/(s)cos(15\º)+84(m)/(s)sin(15\º)-1.633(m)/(s^(2))t`

`102.87(m)/(s)=1.633(m)/(s^(2))t`

`t=(102.87(m)/(s))/(1.633(m)/(s^(2)))`

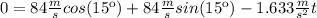
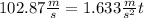
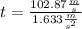
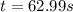`t=62.99s` (6) >>>>This is the time of flight for the golf ball

b) The range (distance traveled by the ball)

For this case, the equation of the distance will be useful (equation 4):

`r=(cos\theta+sin\theta)V_(o).t+(1)/(2)gt^(2)`

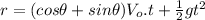
Substiting the value of
`t` found on (6):

`r=(cos(15\º)+sin(15\º))84(m)/(s)(62.99s)-(1)/(2)1.633(m)/(s^(2))}(62.99s)^(2)` (7)

Solving and finding
`r`:

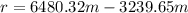`r=6480.32m-3239.65m` (8)

`r=3240.66m` >>>>This is the range of the golf ball