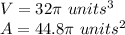1 Answer

Niels Hoogendoorn · Answer 1 · 2020-03-10T03:09:53+0000

For this case we can find the volume and area of the cone:

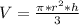
$V = \frac {\pi * r ^ 2 * h} {3}$

Where:

V: It's the volume

A: It's the radius of the base

h: It's the height

We have to:

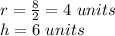
$r = \frac {8} {2} = 4 \ units\\h = 6 \ units$

Substituting:

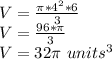
$V = \frac {\pi * 4 ^ 2 * 6} {3}\\V = \frac {96 * \pi} {3}\\V = 32 \pi \ units ^ 3$

On the other hand, the area of the cone is given by:

$A = \pi * r * g +  \pi * r ^ 2$

Where:

A: It's the radio

g: It is the generator of the cone.

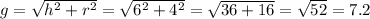
$g = \sqrt {h ^ 2 + r ^ 2} = \sqrt {6 ^ 2 + 4 ^ 2} = \sqrt {36 + 16} = \sqrt {52} = 7.2$

SW:

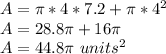
$A = \pi * 4 * 7.2 + \pi * 4 ^ 2\\A = 28.8 \pi + 16 \pi\\A = 44.8 \pi \ units ^ 2$

Answer:

$V = 32 \pi \ units ^ 3\\A = 44.8 \pi \ units ^ 2$

Please log in or register to add a comment.