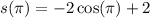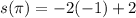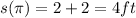Question

If a spring is oscillating (moving) according to the velocity equation v(t) = 2sin(t) (in ft/s), then what is its displacement over its first π seconds of travel?

Answer 1

4 ft

Step-by-step explanation

The velocity equation of the oscillating spring is given by the function.

`v(t)=2 \sin(t) \: \: {ms}^( - 1)`

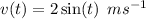
To find the displacement function, we need to to Integrate the velocity function.

`s(t) = \int \: 2 \sin(t) dt`

`s(t) = - 2 \cos(t) + k`

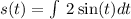
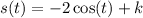
At time t=0, there was no displacement.

This implies that,

`s(0) = 0`

`0= - 2 \cos(0) + k`

`0= - 2 + k`

`k = 2`

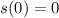
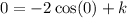
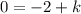
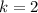
The displacement function then becomes,

`s(t) = - 2 \cos(t) + 2`

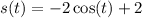
To find the displacement over the first π seconds, we put

`t = \pi`

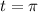
into the equation for the displacement to get,

`s(\pi) = - 2 \cos(\pi) + 2`

`s(\pi) = - 2 ( - 1) + 2`

`s(\pi) = 2 + 2 =4 ft`