Question

Find the center and radius of a circle modeled by the equation x2 + y2 - 4x + 2y - 4 = 0 by completing the square

Answer 1

ANSWER

Center: (2,-1)

Radius: 3 units.

Step-by-step explanation

The given circle has equation:


`{x}^(2) + {y}^(2) - 4x + 2y - 4 = 0`

We rearrange to get;


`{x}^(2) - 4x + {y}^(2)+ 2y =4`

We add the square of half the coefficients of the linear terms to both sides of the equation as shown below:


`{x}^(2) - 4x + {( - 2)}^(2) + {y}^(2)+ 2y + {(1)}^(2) =4+ {( - 2)}^(2)+ {(1)}^(2)`

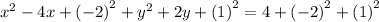
Look out for the perfect squares on the left hand side .


`{(x - 2)}^(2) +{(y + 1)}^(2) =4+ 4+ 1`


`{(x - 2)}^(2) +{(y + 1)}^(2) =9`


`{(x - 2)}^(2) +{(y + 1)}^(2) = {3}^(2)`

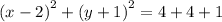
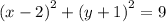
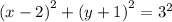
By comparing to :


`{(x - h)}^(2) +{(y - k)}^(2) = {r}^(2)`

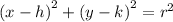
We have the center to be

(h,k)=(2,-1) and radius r=3.